Cirkelprogressioner
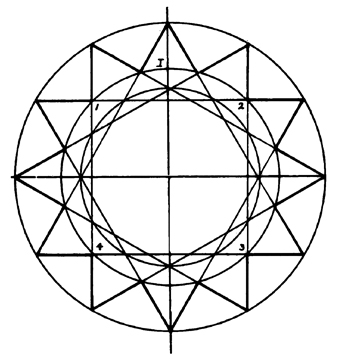
Cirkelprogressioner ved hjælp af kvadratet
eller ved tolvkantens trigoner
Med denne tolvkant-konstruktion som udgangspunkt kan man nu foretage en såkaldt cirkelprogression (eller -regression), dvs. konstruere et system af koncentriske cirkler med voksende eller aftagende radier efter en bestemt metode. Sådanne cirkelsystemer spillede en vigtig rolle i oldtidens (og et stykke op i middelalderens) religiøse forestillinger. Som det snart vil vise sig, har de gamle egyptere benyttet en såkaldt kvadratisk cirkelprogression, og til denne konstruktion har de efter alt at dømme knyttet esoterisk viden af vidtgående betydning.
Udgangspunktet for konstruktionen er den netop omtalte tolvkant på planche IV, fig. 3. De tolv spidser på figuren er sammensat af små ligesidede trekanter, der ligger mellem cirklerne I og II. Disse cirkler kan siges at være forbundet med hinanden ved en tolvstjerneprogression. Denne tolvstjerne overføres til planche V, og her ser man, at tolvstjerneprogressionen også kan opfattes på en anden måde. Som allerede nævnt opstår tolvstjernen ved fire ligesidede trigoner. De horisontale og de vertikale grundlinjer i disse trigoner danner et kvadrat med hjørnepunkterne 1, 2, 3 og 4, og gennem disse går cirkel I. Når denne cirkel tegnes om et kvadrat, vil dette kvadrats hjørner 5, 6, 7 og 8 ligge i den første tolvkantcirkel II.
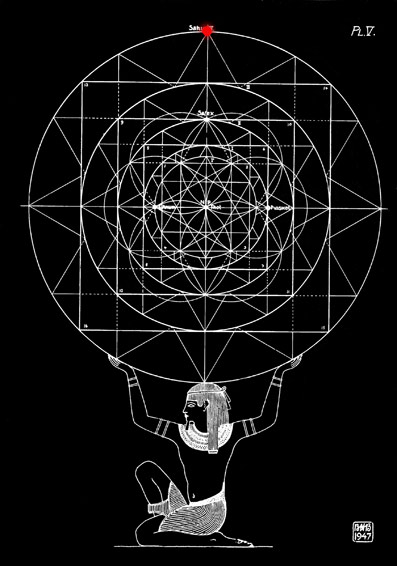
Planche V
Planche-V-PÆLESLAGNING
Planchen kan forstørres ved at klikke på linket herover.
|



